비선형 함수 사용 이유
은닉층에서 이진 활성화 함수를 활성화 함수로 사용할 경우, 다중 출력이 불가능하다는 문제점이 존재한다.
은닉층에서 선형 활성화 함수를 활성화 함수로 사용할 경우, 역전파가 불가능하고 층(layer)을 깊게 쌓는 의미가 사라진다.따라서 은닉층에서 비선형 활성화 함수를 활성화 함수로 사용하는 것이 바람직하다.
시그모이드 함수, Sigmoid(Logit) function
- 출력값이 0과 1 사이
- 출력값의 중심이 12이다. (not zero-centered)
- 입력값이 커질수록 출력값은 1에 가까워지고, 입력값이 작아질수록 출력값은 0에 가까워진다.
- 입력값이 커질수록/작아질수록 기울기(gradient)는 0에 가까워진다.



- 이진 분류(binary classification) 문제에서 출력층에 사용한다.
- Gradient Vanishing 문제가 발생합니다. (학습 성능 ↓)
- exp 함수 사용 시 연산 비용이 크다.
- 학습 속도가 느려질 수 있다.
- 출력값의 중심이 0이 아니기 때문에 발생한다. (not zero-centered)
하이퍼볼릭탄젠트 함수, Tanh(Hyperbolic tangent function)
- 출력값이 -1과 1 사이이다.
- 출력값의 중심이 0이다. (zero-centered)
- 입력값이 작아질수록 출력값은 0에 가까워지고, 입력값이 커질수록 출력값은 1에 가까워진다.
- 입력값이 작아질수록/커질수록 기울기(gradient)는 0에 가까워진다.



- 시그모이드 함수에 비해 학습 성능이 좋다.
- 시그모이드 함수의 최적화 과정이 느려지는 문제를 출력값의 중심을 0으로 만듦으로써 해결했다.
- Gradient Vanishing 문제가 발생한다.
소프트맥스 함수 (Softmax function)
- 출력값이 0과 1 사이다.
- 출력값의 총합이 1이다.
- 소프트맥스 함수는 시그모이드 함수를 일반화 (generalization) 하여 얻을 수 있다.


- 다중 클래스 분류(multi-class classification) 문제에서 출력층에 사용한다.
ReLU, Rectified Linear Unit function
- 입력값이 0보다 작으면 출력값은 0이 되고, 입력값이 0보다 크면 출력값은 가 된다.
- 입력값이 0보다 작으면 기울기(gradient)는 0이고, 입력값이 0보다 크면 기울기(gradient)는 1이다.


- 시그모이드 함수와 하이퍼볼릭탄젠트 함수에 비해 학습 속도가 빠르다.
- 연산 비용이 크지 않다.
- 구현이 간단하다.
- Dying ReLU 문제가 발생한다. (학습 성능 ↓)
- ReLu 함수에서 입력값이 0보다 작을 때 기울기(gradient)가 0이 되어 해당 뉴런이 죽는 것을 말한다.
leaky ReLU
- 입력값이 0보다 작으면 출력값은 가 되고, 입력값이 0보다 크면 출력값은 이 된다.
- 입력값이 0보다 작으면 기울기(gradient)는 0이고, 입력값이 0보다 크면 기울기(gradient)는 .
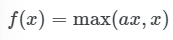
a는 사용자가 설정하는 하이퍼파라미터 (일반적으로 a=0.01)
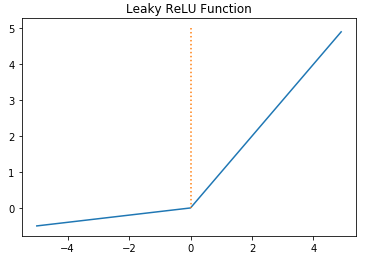
- ReLU 함수에 비해 학습 성능이 좋다.
- 입력값이 0보다 작을 때 기울기(gradient)가 0이 되는 ReLU 함수와 달리 leaky ReLU 함수에서는 입력값이 0보다 작을 때 기울기(gradient)가 0이 되지 않기 때문이다.
- 아주 작은 값(a, 0.01)을 곱하여 Dying ReLU를 막고자 했다.
- 복잡한 분류에서 사용할 수 없다.
- 일부 사례에서 Sigmoid나 Tanh보다 성능이 떨어지기도 한다.
PReLU, Parametric ReLU
- 입력값이 0보다 작으면 출력값은 αx가 되고, 입력값이 0보다 크면 출력값은 x가 된다.
- 입력값이 0보다 작으면 기울기(gradient)는 이고, 입력값이 0보다 크면 기울기(gradient)는 다.
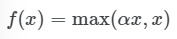
α는 학습해야 하는 파라미터

- leaky ReLU와 달리 α를 가중치 매개변수처럼 학습하여 역전파에서 값이 변경되기에 대규모 이미지 데이터셋에는 ReLU 보다 성능이 좋을 수 있으나, 소규모 데이터셋에선 과적합 발생 위험이 있다.
- 복잡한 분류에 취약하다.
ELU 함수, Exponential Linear Unit function
- 출력값의 중심이 거의 0에 가깝습니다. (zero-centered)
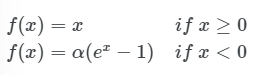
α는 일반적으로 1로 설정한다.

- Dying ReLU 문제를 해결한다.
- ReLU, leaky ReLU와 달리 exp 함수를 계산해야 해서 연산 비용이 크다.
ReLU에 비해 느려서 잘 사용하지 않는다.
- 복잡한 분류에도 사용될 수 있다.
- α=1이면 전 구간에서 변화가 크기 잖아 경사 하강법(Gradient desent)에서 수렴 속도가 빠르다.
- ReLU에 비해 성능이 비약적으로 증가하진 않는다.
SELU, Scaled Exponential Linear Unit
- PReLU 처럼 ELU의 α를 하이퍼 파라미터 값으로 넣어 수정할 수 있게 만든 것이다.
- α를 2개로 학습시키면, 활성화 함수의 분산이 일정해서 성능이 좋아진다.
- α값에 따라 활성화 함수의 결과값이 일정하지 않아 층을 많이 쌓을 수 없다.

- Gradient Vanising 문제를 방지한다.
- Batch normalization과 조합하여 쓰이면 ReLU보다 빠르고 잘 학습될 수 있다.
Maxout
- 활성 함수를 구간 선형 함수(piecewise linear function)로 가정하고, 각 뉴런의 최적화 활성 함수를 학습을 통해 찾는다.
- ReLU의 일반화된 형태로 볼 수 있으며, 성능이 좋다.
- Maxout 활성화 함수 학습을 위해 Maxout unit이라는 구조를 확장한다.
선형 함수 학습하는 선형 노드와 최댓값 출력하는 노드로 구성된다.

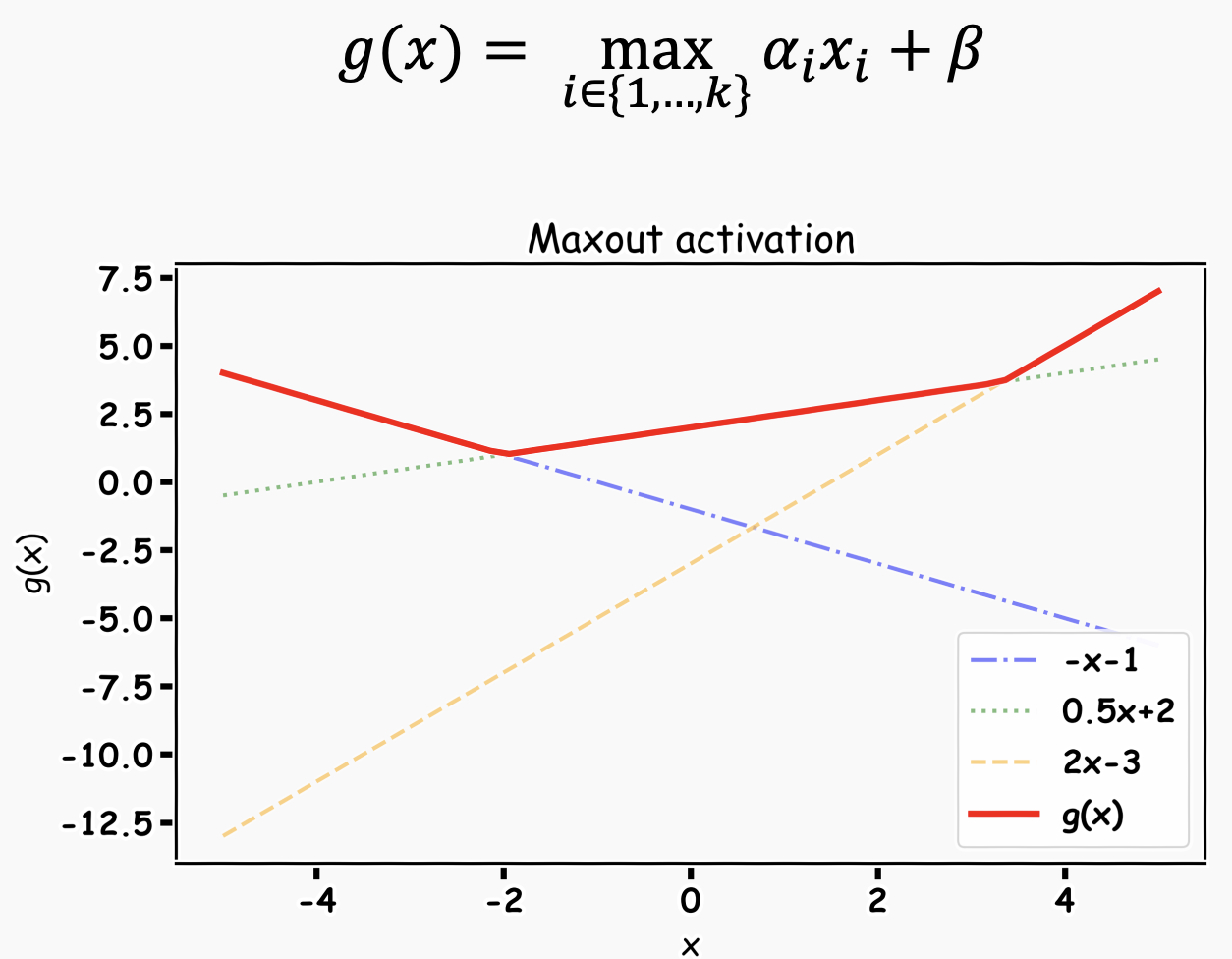
뉴런별로 선형 함수를 여러 개 학습 시킨 뒤 최댓값을 취하면 빨간 선이 나온다.
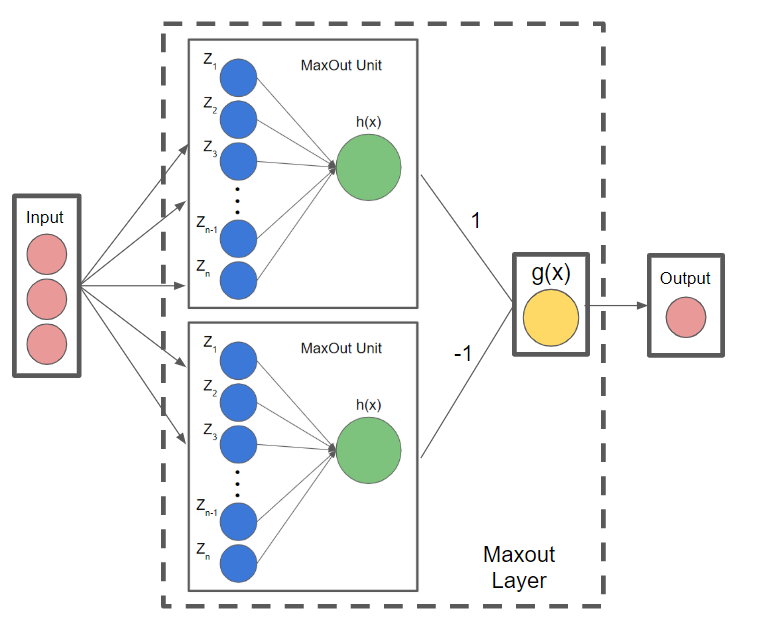
- Dying ReLU 문제를 해결했다.
- 연산 비용이 크다.
- 파라미터의 개수가 두배로 증가하기 때문
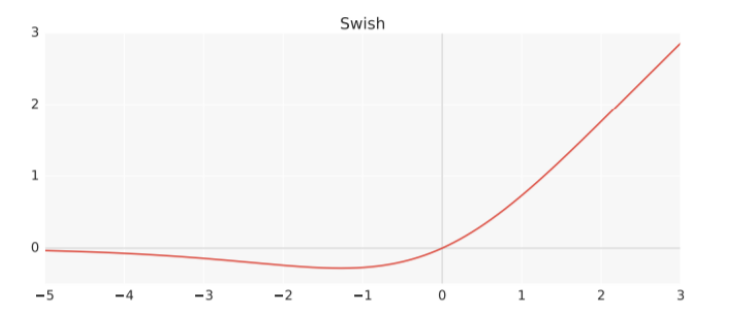
Swish
- Self-Gating으로 인해, 단일 입력만으로도 ReLU를 대체할 수 있다.
- 비단조성이 있기에, 표현력을 증가시키고 gradient flow를 개선시킨다.
- Unboundedness, 학습하는 동안 0 근처에서 gradient 값이 포화되는 것을 막는다.
- Smoothness of the curve, Smooth 함수이므로, 초기값과 learing rate에 덜 민감하다.
- Bounded Below, Swish 함수는 아래로는 하한이 있기 때문에(위로는 상한 X) 강한 regularization 효과를 줄 수 있다.
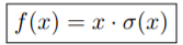
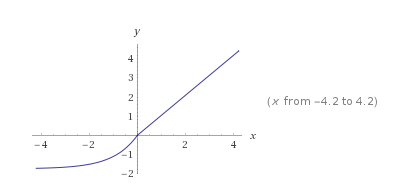
GELU, Gaussain Error Linear Unit
- Computer Vision 분야에서 self-attention 기반의 ViT 같은, 이후의 최신 모델 대부분 GELU를 사용하고 있다.
- 네트워크가 깊어질수록 adaptive dropout 형태로, 입력치에 가중치를 부여하여 zoneout 되는 형태이다.
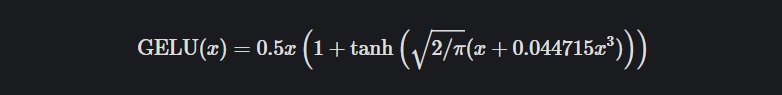
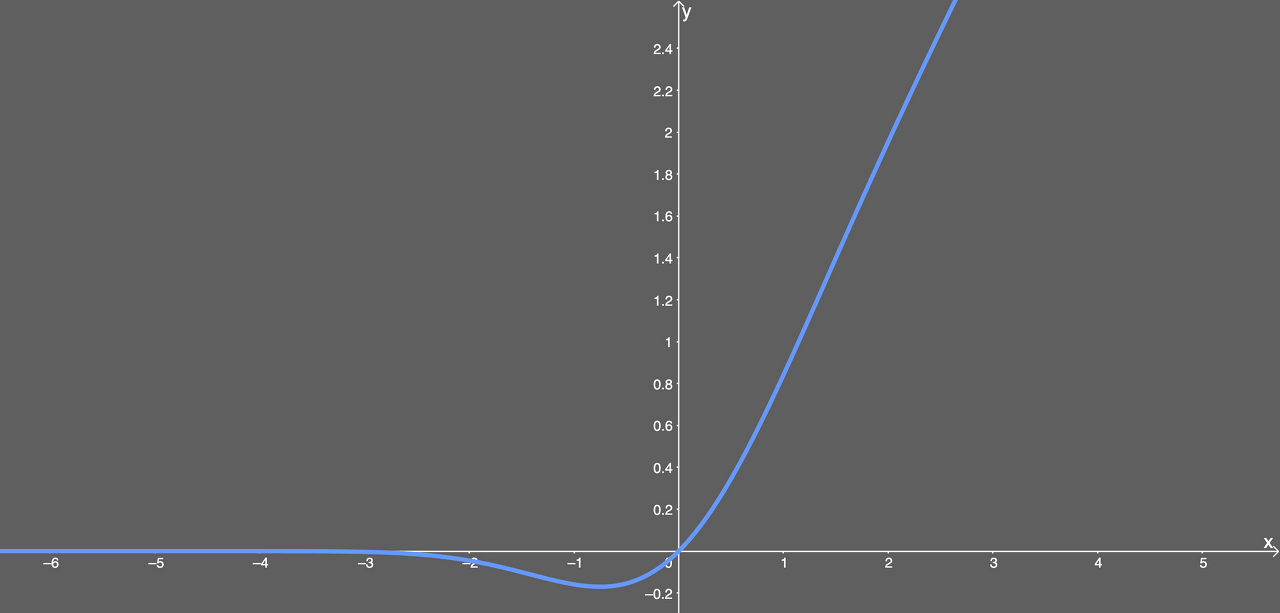


대부분의 경우에서 GELU가 ELU나 ReLU보다 빠르게 수렴하며, 낮은 오차를 보여준다.
SwiGLU
- Residual(Skip) Connection 하기 전, 유의미한 정보 판단을 위한 GLU Gate 앞쪽 절반을 Linear가 아닌, Swish Activation을 통해 비선형 통과시킨다.
- 복잡한 Feature들에 대한 학습율 증대를 기대할 수 있다.
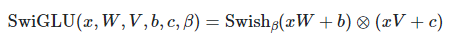
결론
1. 층이 깊어질 수록, 최근 SOTA에서 자주 사용됐던 GELU나 SwiGLU를 사용하는 게 좋아보인다.
2. 그 외에는 ReLU와 ELU를 비교하며 사용하는 게 나아보인다.
Reference
[1] https://shyu0522.tistory.com/m/103
[2] https://itrepo.tistory.com/36
[3] https://cheris8.github.io/artificial%20intelligence/DL-Activation-Function/
[4] https://gooopy.tistory.com/56
[5] https://data-newbie.tistory.com/262
[6] https://velog.io/@cha-suyeon/DL-%ED%99%9C%EC%84%B1-%ED%95%A8%EC%88%98activation-function
[7] https://velog.io/@tajan_boy/Computer-Vision-GELU
'나만 보는 정리노트 > Deeplearning' 카테고리의 다른 글
| ONNX(Open Neural Network Exchange) (0) | 2022.11.30 |
|---|---|
| ANN, DNN, CNN, RNN (0) | 2022.11.17 |
| 분류성능평가지표 (0) | 2022.11.17 |


